Reliably Learning the ReLU in Polynomial Time

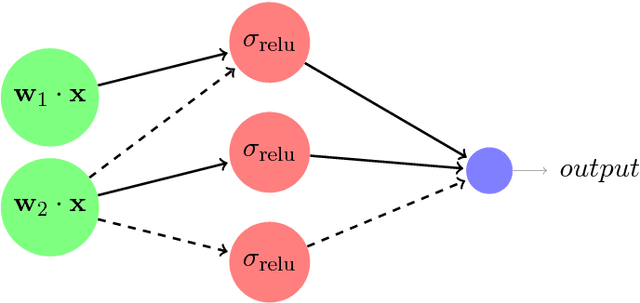
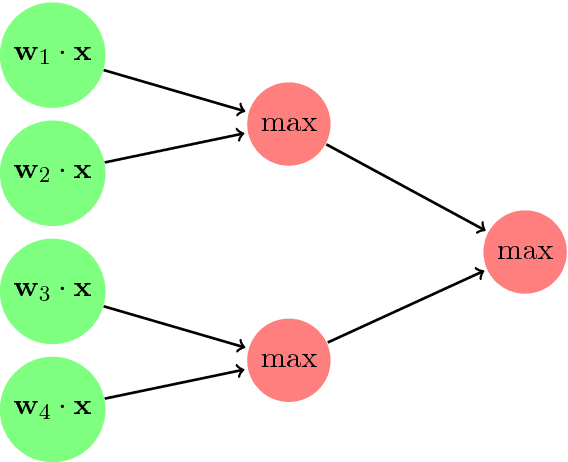
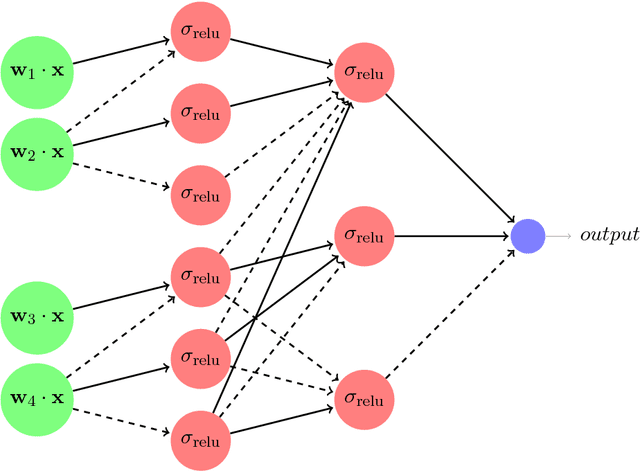
We give the first dimension-efficient algorithms for learning Rectified Linear Units (ReLUs), which are functions of the form $\mathbf{x} \mapsto \max(0, \mathbf{w} \cdot \mathbf{x})$ with $\mathbf{w} \in \mathbb{S}^{n-1}$. Our algorithm works in the challenging Reliable Agnostic learning model of Kalai, Kanade, and Mansour (2009) where the learner is given access to a distribution $\cal{D}$ on labeled examples but the labeling may be arbitrary. We construct a hypothesis that simultaneously minimizes the false-positive rate and the loss on inputs given positive labels by $\cal{D}$, for any convex, bounded, and Lipschitz loss function. The algorithm runs in polynomial-time (in $n$) with respect to any distribution on $\mathbb{S}^{n-1}$ (the unit sphere in $n$ dimensions) and for any error parameter $\epsilon = \Omega(1/\log n)$ (this yields a PTAS for a question raised by F. Bach on the complexity of maximizing ReLUs). These results are in contrast to known efficient algorithms for reliably learning linear threshold functions, where $\epsilon$ must be $\Omega(1)$ and strong assumptions are required on the marginal distribution. We can compose our results to obtain the first set of efficient algorithms for learning constant-depth networks of ReLUs. Our techniques combine kernel methods and polynomial approximations with a "dual-loss" approach to convex programming. As a byproduct we obtain a number of applications including the first set of efficient algorithms for "convex piecewise-linear fitting" and the first efficient algorithms for noisy polynomial reconstruction of low-weight polynomials on the unit sphere.

Distribution-Independent Reliable Learning

We study several questions in the reliable agnostic learning framework of Kalai et al. (2009), which captures learning tasks in which one type of error is costlier than others. A positive reliable classifier is one that makes no false positive errors. The goal in the positive reliable agnostic framework is to output a hypothesis with the following properties: (i) its false positive error rate is at most $\epsilon$, (ii) its false negative error rate is at most $\epsilon$ more than that of the best positive reliable classifier from the class. A closely related notion is fully reliable agnostic learning, which considers partial classifiers that are allowed to predict "unknown" on some inputs. The best fully reliable partial classifier is one that makes no errors and minimizes the probability of predicting "unknown", and the goal in fully reliable learning is to output a hypothesis that is almost as good as the best fully reliable partial classifier from a class. For distribution-independent learning, the best known algorithms for PAC learning typically utilize polynomial threshold representations, while the state of the art agnostic learning algorithms use point-wise polynomial approximations. We show that one-sided polynomial approximations, an intermediate notion between polynomial threshold representations and point-wise polynomial approximations, suffice for learning in the reliable agnostic settings. We then show that majorities can be fully reliably learned and disjunctions of majorities can be positive reliably learned, through constructions of appropriate one-sided polynomial approximations. Our fully reliable algorithm for majorities provides the first evidence that fully reliable learning may be strictly easier than agnostic learning. Our algorithms also satisfy strong attribute-efficiency properties, and provide smooth tradeoffs between sample complexity and running time.